There are three possible outcomes that you may encounter when working with these system of equations:
- one solution
- no solution
- infinite solutions
We are going to try and find values of x, y, and z that will satisfy all three equations at the same time. The following are the equations:
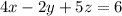
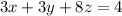
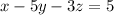
We are going to use elimination(or addition) method
Step 1: Choose to eliminate any one of the variables from any pair of equations.
In this case it looks like if we multiply the third equation by 4 and subtracting it from equation 1, it will be fairly simple to eliminate the x term from the first and third equation.
So multiplying Left Hand Side(L.H.S) and Right Hand Side(R.H.S) of 3rd equation with 4 gives us a new equation 4.:
4. 4x-20y-12z = 20
Subtracting eq. 4 from Eq. 1:
(L.HS) : 4x-2y+5z-(4x-20y-12z) = 18y+17z
(R.H.S) : 20 - 6 = 14
5. 18y+17z=14
Step 2: Eliminate the SAME variable chosen in step 2 from any other pair of equations, creating a system of two equations and 2 unknowns.
Similarly if we multiply 3rd equation with 3 and then subtract it from eq. 2 we get:
(L.HS) : 3x+3y+8z-(3x-15y-9z) = 18y+17z
(R.H.S) : 4 - 15 = -11
6. 18y+17z = -11
Step 3: Solve the remaining system of equations 6 and 5 found in step 2 and 1.
Now if we try to solve equations 5 and 6 for the variables y and z. Subtracting eq 6 from eq. 5 we get:
(L.HS) : 18y+17z-(18y+17z) = 0
(R.HS) : 14-(-11) = 25
0 = 25
which is false, hence no solution exists