Question

What are the coordinates of the orthocenter of △JKL with vertices at J(−4, −1) , K(−4, 8) , and L(2, 8) ?

Answer 1

The orthocenter is
`(-4,8)`

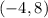
Step-by-step explanation

The orthocenter is the point of intersection of all the altitudes of a triangle.

If it is a right angle triangle then the orthocenter is the point at which the right angle is made.

If it is not a right angle triangle, then you have to find the equations of any two of the altitudes and solve simultaneously.

So you must first check to see if it is a right angle triangle that way you do not have to do bunch work.

The given triangle has vertices
`J(-4,-1)`,
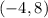`(-4,8)`, and
`L(2,8)`.

`Slope_(JK)=(8--1)/(-4--4)`

`Slope_(JK)=(8+1)/(-4+4)`

`Slope_(JK)=(9)/(0)`

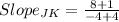
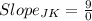
Since the denominator is zero, the slope is undefined.

If the slope of a straight line is undefined, then that line is parallel to the y-axis. In other words, it is a vertical line.

`Slope_(JL)=(8--1)/(2--4)`

`Slope_(JL)=(8+1)/(2+4)`

`Slope_(JL)=(9)/(6)`

`Slope_(JL)=(3)/(2)`

`Slope_(KL)=(8-8)/(2--4)`

`Slope_(KL)=(0)/(2+4)`

`Slope_(KL)=(0)/(6)`

`Slope_(KL)=0`

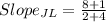
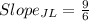
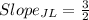
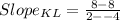
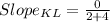
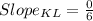
if a straight line has a slope of zero, that line is parallel to the x-axis or it is horizontal.

From the slopes we can see that side KL of the triangle is horizontal and side JK is vertical. This two sides will meet at right angles at K.

See graph.

Therefore the coordinates of K,
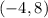`(-4,8)` is the orthocenter of the given triangle.