Question

What are the coordinates of the circumcenter of the triangle? Please show your work <3

Answer 1

We need to find the Circumcenter of the triangle.

Circumcenter could be found by drawing perpendicular bisector of two segments of a triangle.

We have AB a vertical line. So the slope of the vertical line is undefine and slope of perpendicular line to that line would be 0.

We need to find a mid-point between A and B points.

The coordinates of A and B are

A( -2,-5) and B(-2,-2).

So, the Midpoint would be

`9(-2-2)/(2),(-2-5)/(2))  = (-2, -3.5)`

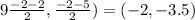
So, the equation of perpendicular line of AB would have slope 0 and it would be

y=-3.5.

Now, let us find perpendicular bisector line of AC.

We have coordinates of A and C points as

A(-2,-5) and C(7,-5)

So, the Midpoint would be

`((-2+7)/(2),(-5-5)/(2))  = (2.5, -5)`

So, the equation of perpendicular line of AC would have slope undefined and it would be

x=2.5.

So, the intersection point of lines x=2.5 and y=-3.5 is (2.5, -3.5).

Therefore, the circumcenter of the triangle is (2.5, -3.5).