Explanation:
HERE,
two equation are,
●-4x+9y=14••••••••••••(equation I)
●12x-10y=-8•••••••••••(equation II)
First multiplying 3 in equation I
we get,
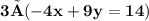
=
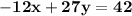 ••(equation III)
••(equation III)
Then,
we combine the equationii and equation III.
we get that,
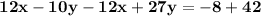
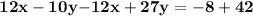



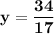

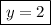
Then,
put the value of y in equation II.
WE get,

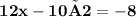





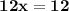

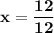


So,
solution of the two equation (-4x+9y) and (12x-10y=-8) is (1,2)