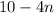Question

1st term in sequence is 6-4th term is -6, the 8th term is -22 write a function that can be used to find the nth term of the sequence

Answer 1

`a_(n)` = 10 - 4n

this is an arithmetic sequence with n th term

`a_(n)` =
`a_(1)` + (n - 1 )d

where
`a_(1)` is the first term and d the common difference

given
`a_(4)` = - 6, then

6 + 3d = - 6 ( subtract 6 from both sides )

3d = - 12 ( divide both sides by 3 )

d = - 4 ← common difference hence

`a_(n)` = 6 - 4 (n - 1 ) = 6 - 4n + 4 = 10 - 4n

Answer 2

Step-by-step explanation

The nth term of the sequence is given by

`U_n=a+(n-1)d`

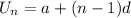
Where

`a`

is the first term and

`d`

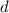
is the constant difference.

We were given that,

`a=6`

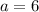
S we just need the common difference to write the nth term.

We can get that from another information given to us.

We were also given that the 4th term is 6. This gives the equation.

`a+3d=-6`

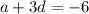
We substitute

`a=6`

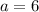
to obtain

`6+3d=-6`

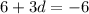
Or

`2+d=-2`

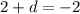
This implies,

`d=-2-2`

`d=-4`

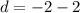
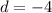
We substitute these values into the general formula to obtain,

`U_n=6+(n-1)*-4`

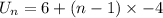
This gives us,

`U_n=6+-4n+4`

`U_n=10-4n`

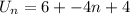
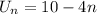
Hence the nth term of the sequence is,

`10-4n`