We are given total 10 tree seedlings.
Number of workshops = 2.
Here order doesn't matters.
When order doesn't matters we apply combination.
We know formula of combination:
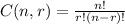
For the given situation, we have
n=10 and r=2.
Plugging values in formula, we get
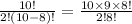
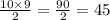
Therefore, 45 different ways can the nursery give out seedlings.