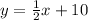Question

The endpoints of a side of rectangle ABCD in the coordinate plane are at A (2, 11) and

B (7, 1). Find the equation of the line that contains the given segment.

The line segment is AD.

What is the Equation?

Answer 1

`2y-x-20=0`

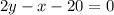
or

`y=(1)/(2)x+10`

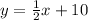
Step-by-step explanation

Let the rectangle be oriented as shown in the diagram.

The line segment AD passes through
`A(2,11)`.

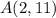All we need now is the slope of AD then we can find its equation.

Since AD is perpendicular t AB, we determine the slope of AB and then use it to find the slope of AD.

`Slope_(AB)=(1-11)/(7-2)`

`Slope_(AB)=(-10)/(5)=-2`

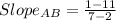
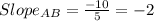
The slope of AD is the negative reciprocal of the slope of AB because they are perpendicular.

`Slope_(AD)=(-1)/(-2)=(1)/(2)`

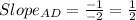
The equation of AD is given by;

`y-y_1=m(x-x_1)`

`y-11=\fra[1}{2}(x-2)`

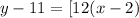
Multiplying through by 2 gives,

`2y-22=(x-2)`

`2y-x-22+2=0`

`2y-x-20=0`

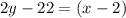
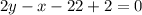
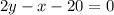
or

`y=(1)/(2)x+10`