If BC bisects BED, this means that BED is split into two equal parts and that CED = BEC. We can see that AD forms a straight line, which means BED and AEB must be supplementary, ow have a sum of 180 degrees. Since CED has the same angle measure as BEC, this means that BED can be found by multiplying as shown:
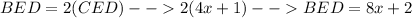
Now find the value of x:
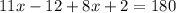
Combine like terms:
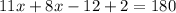
-->
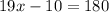
--->
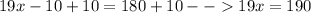
Isolate x -->
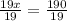
x = 10
Plug in the value of x:
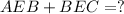
-->
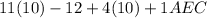
--->
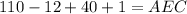
---->

So AEC is 139 degrees.