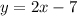Question

Compare the functions represented by the ordered pairs:

Set A: {(5,1), (4,4), (3,9), (2,16), (1,25)} ___________________________

Set B: {(1,-5), (2,-3), (3,-1), (4,1), (5,3)} ___________________________

Answer 1

Set A is a quadratic function :
`y=x^2-12x+36`

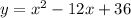
Set B is a linear function:
`y=2x-7`

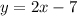
Explanation:

Here set A : {(1,25), (2,16), (3,9), (4, 4) , (5, 1)}

This is a quadratic function

Let

`y=ax^2+bx+c`

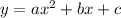
For (1,25) we get
`25=a+b+c` ....(1)

For (2,16) we get
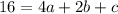`16=4a+2b+c` ....(2)

For (3,9) we get
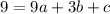`9=9a+3b+c` ....(3)

Subtracting (1) from (2) we get

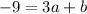`-9=3a+b` .....(4)

Subtracting (2) from (3) we get

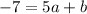`-7=5a+b` ....(5)

Subtracting (4) from (5)

`2a=2`

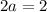
a=1

Substituting a= 1 in (4), we get

`-9=3(1) + b`

`b=-12`

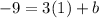
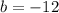
Substituting a = 1 & b = -12 in (1) we get

`c=25-1+12= 36`

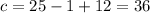
The function is

`y=x^2-12x+36`

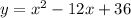
Set B: {(1,-5), (2,-3), (3,-1), (4,1),(5,3)}

This is a linear function

Slope =
`(-3+5)/(2-1)=2`

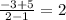
The equation is

`y=2x+c`

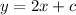
For (1,-5) we get

`-5=2+c`

`c=-7`

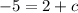
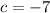
The equation is

`y=2x-7`

Answer 2

We are given

Set A: {(5,1), (4,4), (3,9), (2,16), (1,25)}

We can see that for each x value of the set is increasing exponentially.

We can set up a rule for it y = (6-x)^2

y=(6-5)^2 = (1)^2 = 1

y=(6-4)^2 = (2)^2 = 4

y=(6-3) = (3)^2 = 9

y=(6-2)^2 = (4)^2 = 16

y=(6-1)^2 = (5)^2 = 25.

For set B:

Set B: {(1,-5), (2,-3), (3,-1), (4,1), (5,3)}

It's simply linear function as diffrences of y values are constant that is 2.

We can set a rule for it : y = 2x - 7.

y = 2(1) -7 = 2-7 = -5

y = 2(2) -7 = 4-7 = -3

y = 2(3) -7 = 6-7 = 1

y = 2(4) -7 = 8-7 = 1

y = 2(5) -7 = 10-7 = 3.