Question

Theresa has $26 in her wallet. The bills are worth either $5 or $1. If there are 14 bills in total , How many does she have of each type?

Answer 1

Three $5's and eleven $1's

Explanation:

Answer 2

number of bills worth $5=3,number of bills worth $ 1=11

Explanation:

Hello

we can define two equations to find the number of each type of bill

Step 1

Let

x=number of bills worth $5

y=number of bills worth $ 1

z=total numbers of bills

as described in the question

z=14

hence

x+y=14 ⇒ equation 1

Step 2

Total quantity of money she has in bills of worth $5=5x

Total quantity of money she has in bills of worth $1=1y

w=total she has in her wallet =5x+1y

as described in the question

w=$26

Hence

5x+1 y=26 ⇒ equation 1

Step 3

solve the system of equations

`(1)  x+y=14 \\(2) 5x+1 y=26\\\\`

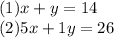
isolating x from each equation

from (1)

`x+y=14\\(Eq\ 3)x=14-y`

Now, from (2)

`5x+1 y=26\\5x=26-y\\`

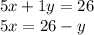
(Eq 3)=(Eq 4), x=x

so

`14-y=(26-y)/(5)`

solving for y

`5(14-y)=26-y\\70-5y=26-y\\70-26=-y+5y\\44=4y\\y=(44)/(4)\\ y=11`

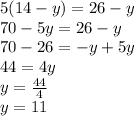
Now replace the value of y in (3) or (4)

`(Eq\ 4)x=(26-y)/(5)\\x=(26-11)/(5)\\x=(15)/(5) \\x=3`

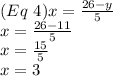
Hence

x=number of bills worth $5=3

y=number of bills worth $ 1=11

Have a nice day