Question

If the shaded area is 23cm^2, then what is the smallest possible value of the inner area?

PLEASE HELP LOL

Answer 1

I suspect it can = 0 when the roots are solved for.

x = 10.44 which is the only positive root. There is another one, but I think it gives a minus number for the white area.

Explanation:

There are two areas that are possible given the dimensions of the two rectangles. The trick is to find both of them. and compare.

Step One

Find the area of the inside rectangle (unshaded area)

Area = (2x - 1)*x Use the distributive property to find the area

Area = 2x^2 - x

Step Two

Find the area of the outside of the frame

Area = (x + 5)(x + 3) Remove the brackets using FOIL

Area = x^2 + 5x + 3x + 15

Area = x^2 + 8x + 15

Step Three

Find the area of the shaded region

Area shaded = x^2 + 8x + 15 – (2x^2 – x) Remove the brackets

Area shaded = x^2 + 8x + 15 – 2x^2 + x Combine like terms

Area shaded = x^2 + 9x + 15 - 2x^2

Area shaded = -x^2 + 9x + 15

Step Four

Find the roots of the quadratic.

a = -1

b = 9

c = 15

Using the quadratic formula, and substituting for a b and c, we get

`\text{x = }\frac{ -b \pm \sqrt{b^(2) - 4ac } }{2a}`

`\text{x = }\frac{ -9 \pm \sqrt{9^(2) - 4*(-1)(15 } }{2(-1)}`

`\text{x = }( -9 \pm √(81  + 4*(1)(15 ) )/(2(-1))`

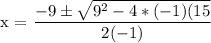
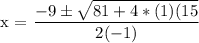
There is only 1 value that works for this problem and that is when x = 10.44