Question

Anyone have the answer to this? Need help ASAP?

Answer 1

f(x) has 3 real roots x = -2, x = 2 and x = 4

complex roots occur in conjugate pairs

x = i is a root then x = - i is a root

there are therefore 2 imaginary roots

f(x) has 3 real roots and 2 imaginary roots

Answer 2

For this case we have the following data:

Polynomial function of grade 5

Given roots: -2, 2,
`4 + i`

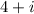
Having an imaginary root given by
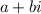`a + bi`, the other root, in the same imaginary way, must be given by its complex conjugate, that is,
`a-bi`.

In this way, the fourth root is given by:

`4-i`

Since the polynomial function is grade 5, it must have 5 roots. Thus, the fifth root must be given by a real number.

Thus, the roots of the polynomial function are given by: three real roots and two imaginary roots.

Answer:

Option D