1 Answer

Simon Byrne · Answer 1 · 2019-12-30T22:39:34+0000

You can use a tangent:

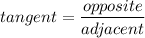
tangent=(opposite)/(adjacent)

We have opposite = 17 and adjacent = x.

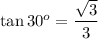
$\tan30^o=(\sqrt3)/(3)$

substitute:

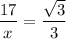$(17)/(x)=(\sqrt3)/(3)$ cross multiply

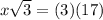$x\sqrt3=(3)(17)$ multiply both sides by √3

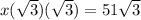
$x(\sqrt3)(\sqrt3)=51\sqrt3$

$3x=51\sqrt3$ divide both sides by 3

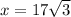
$x=17\sqrt3$

Use the Pythagorean theorem:

$y^2=(17\sqrt3)^2+17^2\\\\y^2=289(\sqrt3)^2+289\\\\y^2=289\cdot3+289\\\\y^2=867+289\\\\y^2=1156\to y=√(1156)\\\\y=34$

-------------------------------------------------------------------------------------------------

Other method.

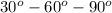30^o-60^o-90^o triangle.

The sides are in the ratio
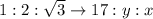
$1:2:\sqrt3\to17:y:x$

Therefore

$17:(2\cdot17):(17\sqrt3)\to17:34:17\sqrt3\to x=34,\ y=17\sqrt3$

Please log in or register to add a comment.