Answer:
The tree is approximately 6.4 feet away from the zip line.
Explanation:
Equation of the line representing the zip line is
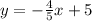
First we need to convert the above equation into
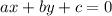 form. So........
form. So........

Thus,
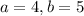 and
and

The formula for distance
 from a point
from a point
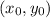 to the line
to the line
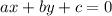 is.........
is.........
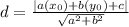
Given that, there is a tree in your yard at the point (4, 10). So here,
 and
and
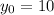
Thus, the distance will be:
 (Rounding to the nearest tenth)
(Rounding to the nearest tenth)
So, the tree is approximately 6.4 feet away from the zip line.