Answer:
The ball can be knocked down at a horizontal distance of 3.09 feet or 102.17 feet from the marshal.
Explanation:
We have the function that represents the height h (x) of the ball

Where x is the horizontal distance of the ball.
We want to find the horizontal distance the ball is at (horizontal distance between the field marshal and the ball) when it is at a height of 10 feet.
To do this, we must do h (x) = 10
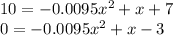
Now we must solve the second degree equation. For this we use the formula of the resolvent:
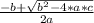
and
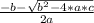
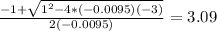 ft
ft
and
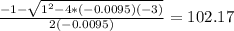 ft
ft
Then, the ball can be knocked down at a horizontal distance of 3.09 feet or 102.17 feet from the marshal.