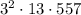Question

Write the prime factorization for 65,169

Answer 1

Let's try to find some primes that divide this number.

The number is not divisible by 2, because it is odd.

The number is divisible by 3 though, because the sum of its digits is:

`6+5+1+6+9=27=3\cdot 9`

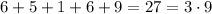
So, we can divide the number by 3 and keep going with the factorization:

`65169/ 3 = 21723`

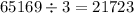
This number is again divisible by 3, because

`2+1+7+2+3 = 15 = 3\cdot 5`

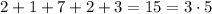
We have

`21723/ 3 = 7241`

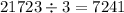
This number is no longer divisible by 3. Let's go on looking for primes that divide it: 5 doesn't because the number doesn't end in 0 nor 5. This number is not divisible by 7 or 11 either (just try). It is divisible by 13 though: we have

`7241/ 13 = 557`

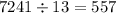
And 557 is prime, so we're done. This means that the prime factorization of 65169 is

`3^2\cdot 13 \cdot 557`