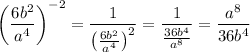Question

(6a^-4b^2)^-2 for the ^ it is an exponent,

Answer 1

Negative exponents work the same as positive ones, except you have to consider the inverse of the base.

So, if for example
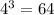`4^3 = 64`, in the same fashion you have

`4^(-3) = (1)/(4^3) = (1)/(64)`

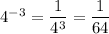
So, negative exponents lead to a fraction with numerator 1 and denominator the same expression, but with positive exponent.

So, in your case, let's work with the inner parenthesis first:

`6a^(-4)b^2 = 6 (1)/(a^4)b^2 = (6b^2)/(a^4)`

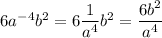
Now, if we want to raise this to the negative two, we have

`\left((6b^2)/(a^4)\right)^(-2) = (1)/(\left((6b^2)/(a^4)\right)^2)} = (1)/((36b^4)/(a^8)) = (a^8)/(36b^4)`