Answer:
The shortest distance between checkpoint A and checkpoint B is 23.33 yards.
Explanation:
We are given the following information in the question:
Let O be the starting point.
Distance between the starting point and checkpoint A = 20 yards
To reach checkpoint B, one need to take a turn and let it be a 90 degrees turn toward right or left.
Distance between checkpoint A and checkpoint B = 12 yards
In order to find the shortest distance between the checkpoint A and checkpoint B, the displacement, we use the Pythagoras theorem.
Statement:
In a right angled triangle:
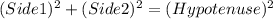
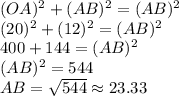
Hence, the shortest distance between checkpoint A and checkpoint B is 23.33 yards.