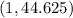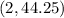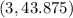ANSWER
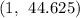
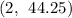
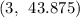
Step-by-step explanation
We chose a value for
 and substitute in to the equation and solve for
and substitute in to the equation and solve for
 .
.
If Jon works for
 hour,
hour,
Then the equation becomes,
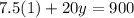
We make
 the subject
the subject


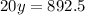
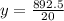
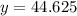
If Jon works for
 hours,
hours,
Then the equation becomes,
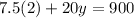
We make
 the subject
the subject
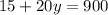
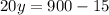
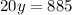
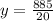
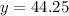
If Jon works for
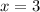 hours,
hours,
Then the equation becomes,
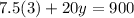
We make
 the subject
the subject
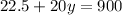
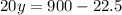
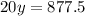
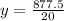
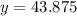
Therefore three combinations of hours worked and lawns mowed are