Given
The expression is given in the question

Find the expression is equivalent to the above expression.
To proof
As expression is given in the question

By using the properties
product of powers property tells us that when you multiply powers with the same base you just have to add the exponents.
i.e
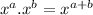
Now using this in above
we get
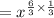
Also by using the property
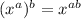
We get
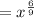
Therefore expression becomes
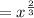
Hence proved