Question

Hunter and Brian are creating a poster for a project and they need to combine two different size boards to create their project. If the total area cannot exceed 7x to the second power -6x+2 square inches and one board Is 2x to the second power -9x+8 square inches, then what must be the maximum area of the second board?

Answer 1

5x² + 3x - 6

Explanation:

Data:

• Total area: 7x² - 6x + 2

• Area of one board: 2x² - 9x + 8

• Area of the other board: f(x)

The addition of the area of the two boards cannot exceed the total area. Then:

f(x) + 2x² - 9x + 8 ≤ 7x² - 6x + 2

f(x) ≤ 7x² - 6x + 2 - 2x² + 9x - 8

f(x) ≤ (7x² - 2x²) + (-6x + 9x) + (2 - 8)

f(x) ≤ 5x² + 3x - 6 in square inches

Answer 2

The maximum area of the second board must be
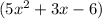`(5x^2+3x-6)` square inches.

Explanation:

The total area of two different size boards cannot exceed
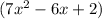`(7x^2-6x+2)` square inches.

The area of one board is
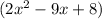`(2x^2-9x+8)` square inches.

Suppose, the area of the second board is
`y` square inches.

That means......

`y+(2x^2-9x+8)\leq 7x^2-6x+2\\ \\ y\leq (7x^2-6x+2)-(2x^2-9x+8)\\ \\y \leq 7x^2-6x+2-2x^2+9x-8\\ \\ y\leq 5x^2+3x-6`

So, the maximum area of the second board must be
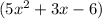`(5x^2+3x-6)` square inches.