the average of "arithmetic mean" of a dataset is simply the "sum of the data" divided by the "amount of data", so if we had say
a, b, c
its average will be (a+b+c)/3
so, let's say Lucy will need to earn "x" to have an average of $600, so
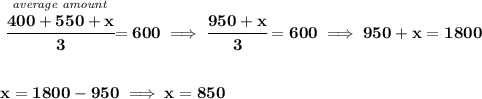
so, if she earns that much more, she'll have an average of 600, and if she earns more than that, her average is "more than 600" then.
x ⩾ 850.