Answer:
Domain:
![[-1,0]\cup [1,\infty )](https://img.qammunity.org/2019/formulas/mathematics/middle-school/7lapu3b1h6x9t11yqh0hwlk1vqjki25063.png)
Explanation:
Since we know that a square root function is not defined for negative numbers. In order our function to be defined values inside radical must be greater than or equal to zero.
Our function will be defined when
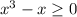
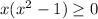

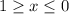 or
or
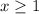
Now we will use number line method of solving inequalities to check whether our answer is right or not.
Let us try -2, -1/2, 1/2 and 2 to check which conditions meet our criteria.

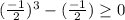
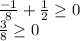
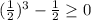
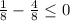
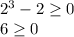
Therefore, we can see that our function is defined when
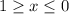 or
or
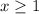 and domain of f(x) is
and domain of f(x) is
![[-1,0]\cup [1,\infty )](https://img.qammunity.org/2019/formulas/mathematics/middle-school/7lapu3b1h6x9t11yqh0hwlk1vqjki25063.png) .
.