Question

two high school students are hired to rake leaves. They will work a couple hours each afternoon until the job is completed. They can choose one of the two payment plans. Plan A pays $11.50 per afternoon, while Plan B pays 2 cents for one day of work, 4 cents total for two days of work, 8 cents for three days of work, 16 cents total for four days, and so on. Each student chooses a different plan. On which day would their total pay be approximately the same?

Answer 1

x = 14 days

Explanation:

To answer the question, find a function that represents the payment mode of plan A and an equation that represents the mode of payment of plan B.

For Plan B the payment is constant every afternoon, $ 11.5 (or 1150 cents) so the equation to represent this form of payment is as follows:

A = 1150x (with units in cents)

This equation represents the line of a line of slope 1150, which passes through point (0,0). Where x is the number of days {1, 2, 3 ....}

In form of payment B, the amount of payment is doubled each day. And the first payment is 2 cents. Therefore this model is represented by an exponential base 2 equation of the form:

`B = (2) ^ x`

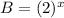
Where x represents the number of days, which is always greater than 0 {1, 2, 3, 4 ...}

To know in which day the salary will be approximately the same we equate both equations and we clear x.

A = B

`1150x = (2) ^ x\\1150x- (2) ^ x = 0`

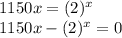
It is a somewhat difficult equation to solve, so I recommend iterating to get a value where the function approaches 0 (when this difference is zero it means that the A and B salaries are the same).

Suppose

x = 13 days

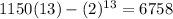`1150(13) - (2) ^ {13} = 6758`cents

It is not equal to 0.

Let's try with x = 15

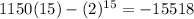`1150(15) - (2) ^ {15} = -15518` cents

Then the value that makes the function zero is between x = 13 and x = 15

Let's try with x = 14

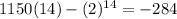`1150(14) - (2) ^ {14} = -284` cents = 2.84 $ difference. X = 14 is the whole number where functions A and B are closer together (the salary is approximately the same). Therefore the answer is

x = 14 days