Question

an astronaut has a mass of 100 kg and has a weight of 370N on Mars. what is the gravitational strength on Mars?

Answer 1

The gravitational strength of the mars will be 3.7 m/s^2

Step-by-step explanation:

Answer 2

Weight of the object on surface of any planet is given as the gravitational pull on the object due to planet

This gravitational pull is defined as formula below

`F = mg`

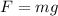
m = mass of object

g = acceleration due to gravity of the planet

now here it is given that weight on the planet is 370 N which is defined as the force due to planet

Also the mass is given as 100 kg

now using the formula above

`370 = 100 * g`

`g = (370)/(100)`

`g = 3.7 m/s^2`

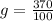
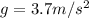
so the gravitational strength of the mars will be 3.7 m/s^2