Question

The graph shows a distribution of data.

What is the variance of the data?

- 0.0625
- 0.25
- 0.5
- 1.5

Answer 1

To find the variance of data, calculate the average of the squared differences between each data point and the mean.

Step-by-step explanation:

To find the variance of the data, we need to calculate the average of the squared differences between each data point and the mean. To do this, follow these steps:

1. Find the mean of the data by adding up all the data points and dividing by the total number of data points.
2. Subtract the mean from each data point and square the result.
3. Add up all the squared differences.
4. Divide the sum of squared differences by the total number of data points.

Based on the given options, we don't have enough information to calculate the variance.

Answer 2

The curve is bell shaped, the distribution of data is equal on both sides , that is from mid point called mean.

50% of Data lies on both side of mean.

So,Equation 1.→ Mean - 2 × standard deviation=3.5

or,Equation 2. →Mean + 2 × standard deviation=4.5

x -2 a= 3.5

4 -2 a=3.5

4-3.5=2 a

2 a=0.5

`a=(0.5)/(2)=0.25`

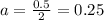
Using equation (2)

→ 4 +2 a=4.5

2 a=4.5-4

2 a=0.5

`a=(0.5)/(2)=0.25`

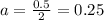
So, Standard Deviation = 0.25

→Variance =(Standard deviation)²=a²=(0.25)²=0.0625

Option (A)→0.0625