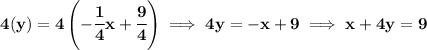Question

Write an equation of the line that passes through (−3,3) and is perpendicular to the line 2y=8x−6.

Answer 1

keeping in mind that perpendicular lines have negative reciprocal slopes, so hmmm wait a second, what is the slope of 2y=8x−6. anyway?

`\bf 2y=8x-6\implies y=\cfrac{8x-6}{2}\implies y=\cfrac{8x}{2}-\cfrac{6}{2}\\\\\\y=\stackrel{\downarrow }{4}x-3\impliedby \begin{array}ll\cline{1-1}slope-intercept~form\\\cline{1-1}\\y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}}\\\\\cline{1-1}\end{array}`

`\bf ~\dotfill\\\\\stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}}{\stackrel{slope}{4\implies \cfrac{4}{1}}\qquad \qquad \qquad \stackrel{reciprocal}{\cfrac{1}{4}}\qquad \stackrel{negative~reciprocal}{-\cfrac{1}{4}}}`

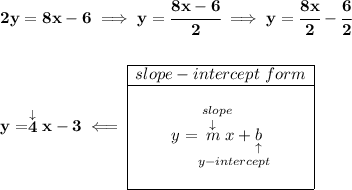
so, we're really looking for the equation of a line whose slope is -1/4 and runs through (-3, 3).

`\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{3})~\hspace{10em}slope = m\implies -\cfrac{1}{4}\\\\\\ \begin{array}\cline{1-1}\textit{point-slope form}\\\cline{1-1}\\y-y_1=m(x-x_1)\\\\\cline{1-1}\end{array}\implies y-3=-\cfrac{1}{4}[x-(-3)]\implies y-3=-\cfrac{1}{4}(x+3)\\\\\\y-3=-\cfrac{1}{4}x-\cfrac{3}{4}\implies y=-\cfrac{1}{4}x-\cfrac{3}{4}+3\implies y=-\cfrac{1}{4}x+\cfrac{9}{4}`

now, that equation is fine, is in slope-intercept form, and we can do away with the denominators by simply multiplying both sides by the LCD of all fractions, in this case , 4, and put the equation in standard form instead.

standard form for a linear equation means

- all coefficients must be integers

- only the constant on the right-hand-side

- "x" must not have a negative coefficient

`\bf 4(y)=4\left( -\cfrac{1}{4}x+\cfrac{9}{4} \right)\implies 4y=-x+9\implies x+4y=9`

Answer 2

4y = -x + 9

Explanation:

2y = 8x - 6

Divide through by 2:-

y = 4x -3 so the slope of this line = 4

Slope of the line perpendicular to this = -1/4

So using the point/slope form of an equation of a line and the point (-3,3) we have:-

y - 3 = -1/4(x - -3)

y = -1/4x - 3/4 + 3

y = -1/4 x + 9/4 Multiply through by 4:-

4y = -x + 9