Question

How do I solve 0=-2/3x^(-5/3)+8/3x^(-2/3)?

Answer 1

Answer: The solution of the given equation is
`(1)/(4)`.

Step-by-step explanation:

The given equation is,

`(2)/(3)x^{ -(5)/(3)} +(8)/(3)x^{ -(2)/(3)}=0`

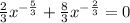
It can be written as,

`\frac{2}{3x^{ (5)/(3)}} +\frac{8}{3x^{ (2)/(3)}}=0`

`\frac{8x^{(5)/(3)}-2x^{(2)/(3)}}{3x^{(7)/(3)}}=0`

`8x^{(5)/(3)}-2x^{(2)/(3)}=0`

`2x^{(2)/(3)}(4x-1)=0`

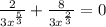
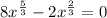
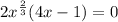
Equate each factor equal to 0. Then we get,

`x=0` and
`(1)/(4)`

Since the power of x is in negative, so the equation is not defined for x = 0.

Therefore the only solution of the given equation is
`(1)/(4)`.