Question

Complete the statements about the figures shown in the graph.

Quadrilateral ABCD undergoes a (blank) to form quadrilateral A′B′C′D′.
Quadrilateral ABCD undergoes a (blank) to form quadrilateral A″B″C″D″.

Answer 1

Reflection and a Translation

Answer 2

Quadrilateral ABCD reflect across x-axis to form quadrilateral A′B′C′D′.

Quadrilateral ABCD translate 7 units left and 1 unit down to form quadrilateral A'′B'′C′'D′'.

Explanation:

From the given figure it is clear that the vertices of ABCD are A(3,4), B(4,3), C(5,1) and D(1,2).

The vertices of A'B'C'D' are A'(3,-4), B'(4,-3), C'(5,-1) and D'(1,-2).

The relation between ABCD and A'B'C'D' is defined by rule

`(x,y)\rightarrow (x,-y)`

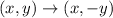
Therefore, the quadrilateral ABCD reflect across x-axis to form quadrilateral A′B′C′D′.

The vertices of A''B''C''D'' are A''(-4,3), B''(-3,2), C''(-2,0) and D''(-6,1).

The relation between ABCD and A''B''C''D'' is defined by rule

`(x,y)\rightarrow (x-7,y-1)`

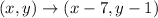
Therefore, the quadrilateral ABCD translate 7 units left and 1 unit down to form quadrilateral A'′B'′C′'D′'.