Question

OM is a common external tangent to circles K and L at poinys O and N, respectively. If JK = 12 and LN =8, find NM to the nearest hundredth by completing the following steps

Answer 1

Answer: Value of NM=41

Explanation:

Since we have given that

JK =12 cm which is the measure of the radius

so,

KO=12 cm also.

And we have given that

LN= 8cm

KL=12+8=20

Let LM be x

Construction : Join KO and LN such that KO║LN.

Now, We can use the BPT (Basic proportionality theorem)

`(LN)/(KO)=(LM)/(KM)\\\\(8)/(12)=(x)/(x+20)\\\\(2)/(3)=(x)/(x+20)\\\\2x+40=3x\\\\x=40`

Now, if we consider ΔLMN,

using Pythagorus theorem,

`LM^(2) +LN^2=NM^2\\\\40^2+8^2=NM^2\\\\1600+64=NM^2\\\\1664=NM^2\\\\√(1664)=NM\\\\NM=40.8=41`

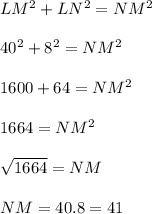
Hence, Value of NM=41