Question

Carlota wrote the equation y + 1 = 2 (x - 3) for the line passing through the points (-1, 3) and (2, 9). Explain and correct her error.

Answer 1

For this case we have the following equation:

`y + 1 = 2 (x - 3)`

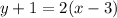
That can be rewritten in the form
`y = mx + b`

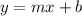
Where:

• m is the slope of the line

• b is the cut point

So, we have:

`y + 1 = 2 (x - 3)\\y + 1 = 2x-6\\y = 2x-6-1\\y = 2x-7`

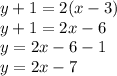
Where:

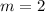`m = 2` is the slope

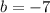`b = -7` is the cut point

Carlota has the following points:

(-1, 3) and (2, 9)

To know if the line
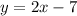`y = 2x-7` passes through these points, we must replace them in the equation and the equality must be fulfilled. So:

Point (-1, 3):

Substituting:

`3 = 2 (-1) -7\\3 = -2-7`

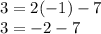
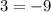`3 = -9` It's false, equality is not met. The point (-1, 3) does not go through the line.

The equation written by Carlota is erroneous, the procedure to follow is:

Given
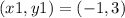`(x1, y1) = (- 1, 3)` and
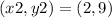`(x2, y2) = (2, 9)`, we find the slope:

`m=((y2-y1))/((x2-x1))`

`m=((9-3))/((2-(-1)))`

`m=(6)/(3)`

`m=2`

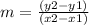
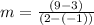
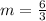
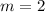
We observe that the slope found by Carlota is the same. Let's see cut point "b". For this we substitute any of the points given in the equation:

`y = 2x + b`

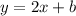
Substituting (2,9) we have:

`9 = 2 (2) + b\\9 = 4 + b\\b = 9-4\\b = 5`

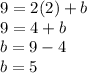
Thus, Carlota's error was at the cut-off point. The correct equation of the line that passes through the given points is
`y = 2x + 5`

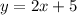
Answer:

The correct equation of the line that passes through the given points is
`y = 2x + 5`

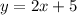
Carlota's mistake was at the cutoff point