Answer: The correct option is second, i.e. ,"2 times the integral from 0 to 1 of the quantity x cubed minus 3 times x squared plus 2 times x, dx".
Step-by-step explanation:
The given equation is,
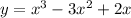
It can be written as,
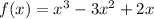
Find the zeros of the equation. Equation the function equal to 0.
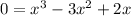
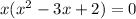

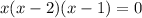
So, the three zeros are 0, 1 and 2.
The graph of the equation is shown below.
From the given graph it is noticed that the enclosed by the curve and x- axis is lies between 0 to 2, but the area from 0 to 1 lies above the x-axis and area from 1 to 2 lies below the x-axis. So the function will be negative from 1 to 2.
The area enclosed by curve and x-axis is,
![A=\int_(0)^(1)f(x)dx+\int_(1)^(2)[-f(x)]dx](https://img.qammunity.org/2019/formulas/mathematics/high-school/m2vcso2d6s7z2jfdzkdvem6xjx00605a3g.png)
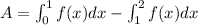
From the graph it is noticed that the area from 0 to 1 is symmetric or same as area from 1 to 2. So the total area is the twice of area from 0 to 1.

![A=2\int_(0)^(1)[x^3-3x^2+2x]dx](https://img.qammunity.org/2019/formulas/mathematics/high-school/vpqz2t6mcm77nbilqz4kl5f2pk1z1v5nsv.png)
Therefore, The correct option is "2 times the integral from 0 to 1 of the quantity x cubed minus 3 times x squared plus 2 times x, dx".