The function and it's inverse are graphed in the attached diagram.
For y -intercept is

. This implies
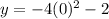
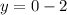
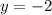
For x-intercept,
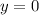
, This means that,
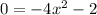
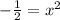
The above equation tells us that, the above equation has no real roots. Hence the graph has no x-intercept.
Also the value
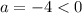
, tells us the graph is a maximum graph.
THE INVERSE OF y
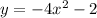
Interchange x and y.
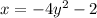
Make y the subject to obtain,
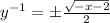
.
for x<-2.
You can now find the intercepts, with some few points to graph the inverse.