Answers:
15) x = 8,
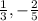
16) x = 9,
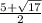 ,
,
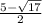
17) x = 6,
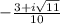 ,
,

Explanation:
15x³ - 119x² - 10x + 16 = 0

So, the possible rational roots are: +/-
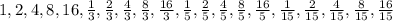
Use synthetic division with each one until you find a remainder of zero. I am not going to go through each one because it is too time consuming, however, the first one that works is x = 8
(x - 8)(15x² + x - 2)
Next, factor 15x² + x - 2 using any method
(x - 8)(3x - 1)(5x + 2)
Now, solve for x.
x = 8, x =
 , x =
, x =
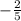
*******************************************************************
For #16 & 17, follow the same process as above.