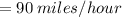Question

Train a And train b leave Central Station at the same time they travel the same speed but in opposite direction with a train a heading towards Station a and train b heading towards station b train a Reaches station after 2 1/2 hours train b reaching station be after four hours you station A and b Station are 585 miles apart what is the rate of the trains

Answer 1

The total distance between the two stations is

`585 miles`

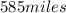
Let the distance between the Central Station and station b be x

This implies that the distance between the Central Station and station a is

`(585 - x) \: miles`

`speed=(distance)/(time)`

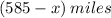
so, let us write equations in terms of speed for the two trains and solve

For train a,

`speed=(585 - x)/(4 ) ....eqn \: 1`

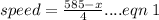
For train b,

`speed=(x)/(2  (1)/(2) ) .....eqn \: 2`

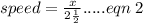
We were told that both trains traveled with the same speed

This means that eqn 1 = eqn 2

`(585 - x)/(4 )=(x)/(2.5)`

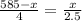
Cross multiplying

`2.5(585 - x)=4(x)`

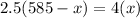
Expanding the brackets

`1462.5  - 2.5x =4x`

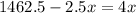
Grouping like terms

`1462.5= 4x + 2.5x`

`6.5x = 1462.5 \\ x = (1462.5)/(6.5 ) =225 \: miles`

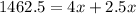
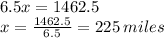
The speed at which the trains were travelling is

`(225)/(2.5)= 90 \: miles /hour`

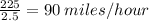
Hence the rate of the trains is

`=90\: miles /hour`

Answer 2

Both trains are traveling at 90 miles per hour.

Explanation:

We are told that the rate is the same for both trains, and we know that the distance traveled by train a plus the distance traveled by train b equals 585 miles.

We will use
`Distance=Rate* Time` formula to solve this problem.

Train A:
`D_a=R*2.5` (Using 2.5 instead of 2 and 1/2)

Train B:
`D_b=R*4`

We can set an equation to solve for rate R of trains as:

`D_a+D_b=585`

`2.5R+4R=585`

`6.5 R=585`

`R=(585)/(6.5)`

`R=90`

Therefore, rate of both train a and train b is 90 miles per hour.