Question

What isn’t the minimum value of c=7x+8y given the constraints on x and y listed below

2x+y>=8
x+y>=6
x>=0
y>=0

A)32
B)42
C)46
D)64

Please please please explain how you got it

Answer 1

we have to find minimum value of c=7 x+8 y

Constraints are

2x+y>=8

x+y>=6

x>=0

y>=0

The points which satisfy the above inequality is (2,4),(6,0),(0,8).

At (2,4) , C= 7×2+8×4=14+32=46

At(6,0), C=7×6+8×0=42

At (0,8), C=7×0+8×8=64

So option A which is 32 is not the minimum value of C=7 x+ 8 y.

Answer 2

32 is not minimum value of C

Explanation:

Given constraints:

`2x+y\geq8`

`x+y\geq8`

`x\geq8`

`y\geq8`

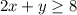
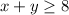
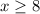
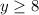
Now we draw the graph of each constraint and see the feasible region in graph. Please have a look attached graph.

We got three corner points A(0,8) B(2,4) and C(6,0)

Now we find the optimal solution for each value of corner points.

C(0,8)=7(0)+8(8)=64

C(2,4)=7(2)+8(4)=14+32=46

C(6,0)=7(6)+8(0)=42

Option A is correct. 32 is not minimum value of C