Question

Graph y=sin^-1(1/4)x) on the interval -5<x<5

Answer 1

D is the answer I just took the test.

Answer 2

we are given

`y=sin^(-1)((1)/(4)x)`

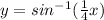
We can select some values between x=-5 and x=5

and then we can plug it and find y

after that we get points

and then we can locate it on the graph and join them to get graph

At x=-4:

`y=sin^(-1)((1)/(4)(-4))`

`y=-1.5708`

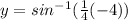
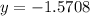
point is (-4,-1.57080)

At x=-3:

`y=sin^(-1)((1)/(4)(-3))`

`y=-0.84806`

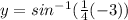
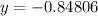
point is (-3,-0.84806)

At x=-2:

`y=sin^(-1)((1)/(4)(-2))`

`y=-0.52360`

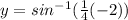
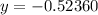
point is (-2,-0.52360)

At x=-1:

`y=sin^(-1)((1)/(4)(-1))`

`y=-0.25268`

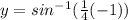
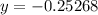
point is (-1,0.25268)

At x=0:

`y=sin^(-1)((1)/(4)(0))`

`y=0`

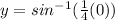
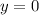
point is (0,0)

At x=1:

`y=sin^(-1)((1)/(4)(1))`

`y=0.25268`

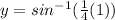
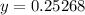
point is (1,0.25268)

At x=2:

`y=sin^(-1)((1)/(4)(2))`

`y=0.52360`

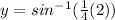
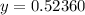
point is (2,0.52360)

At x=3:

`y=sin^(-1)((1)/(4)(3))`

`y=0.84806`

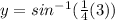
point is (3,0.84806)

At x=4:

`y=sin^(-1)((1)/(4)(4))`

`y=1.57080`

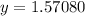
point is (4,1.57080)

now, we can locate these values

we get our graph as