we are given
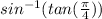
Let's assume entire term as x
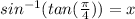
now, we can take both sides as sin
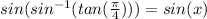
since, sin and sin^-1 are inverse of each other
so, they will get cancelled
and we get

now, we know that
tan(pi/4)=1
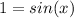
and sin is 1 at pi/2
so, we get

so, option-D.........Answer