Question

Please answer these I need help! 1-5 questions.

1: What is the range of the data set?
27, 5, 11, 13, 10, 8, 14, 18, 7
A. 22
B. 7.5
C. 11
D. 16

2. Use the list below to find the lower quartile.
27, 5, 11, 13, 8, 14, 18, 7
A. 7
B. 7.5
C. 8
D. 8.5

3. Use the list below to find the upper quartile.
27, 5, 11, 13, 10, 8, 14, 18, 7
A. 11
B. 13
C. 14
D. 16

4. What is the interquartile range of this data set?
5, 5, 6, 7, 9, 11, 14, 17, 21, 23
A. 7
B. 9
C. 11
D. 13

5. What is the interquartile range of this data set?
4, 5, 7, 9, 10, 14, 16, 24
A. 6
B. 7
C. 8
D. 9

Please help!

Answer 1

1. 22

2. 7.5

3. 16

4. 11

5. 8.5

Explanation:

1) Given data set : 27, 5, 11, 13, 10, 8, 14, 18, 7

To find : Range

Solution :

Range refers to the difference between the largest and smallest term in a given data set.

Here,

largest term = 27

smallest term = 5

Therefore, Range = 27 - 5 = 22

2) In increasing order, we can write this data as 5, 7, 8, 11, 13, 14, 18, 27

The lower quartile, denoted by
`Q_1` is the value of median of the lower half of a data set .

Now, the lower half of the data is, {5, 7, 8, 11}, so the lower quartile is the median of {5, 7, 8, 11} .

As number of terms in lower half of the data is even, median is the mean of middle values i.e,
`(7+8)/(2)=(15)/(2)=7.5`

3)

The upper quartile denoted by
`Q_3` is the median of the upper half of a data set.

Now, the upper half of the data is, {5, 7, 8, 11} , so the upper quartile is the median of {13, 14, 18, 27}

As the number of terms is even, upper quartile is the mean of middle values

i.e,
`(14+18)/(2)=(32)/(2)=16`

4) Given data : 5, 5, 6, 7, 9, 11, 14, 17, 21, 23

First half set = 5, 5, 6, 7, 9

Second half set = 11, 14, 17, 21, 23

`Q_1=6\\Q_3=17`

We know that interquartile range =
`Q_3-Q_1` = 17 - 6 = 11

5) Given data : 4, 5, 7, 9, 10, 14, 16, 24

lower half of the data : 4, 5, 7, 9

upper half of the data : 10, 14, 15, 24

`Q_1=(5+7)/(2)=6\\Q_3=(14+15)/(2)=(29)/(2)=14.5`

Therefore, interquartile range =
`Q_3-Q_1=14.5-6=8.5`

Answer 2

1)

First arrange the data set in increasing order; 5, 7, 8, 10, 11, 13, 14, 18, 27

Range: The difference between the largest and smallest data in a data set.

From the above data, we have the largest data is 27 and smallest data is 5

Range=largest-smallest=27-5=22

therefore, the range for the given data is, 22.

2)

Write the data in increasing data; {5, 7, 8, 11, 13, 14, 18, 27}

Notice that there are 8 values, which is even.

Then the middle data values are the 4th value from the left and the 4th value from the right, i.e, 11 and 13.

The median is the mean of the two middle values,

`Median=(11+13)/(2)=(24)/(2) =12`

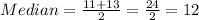
The lower half of a data set is the set of all values that are to the left of the median value when the data is in the increasing order.

The Upper half of a data set is the set of all values that are to the right of the median value when data is in increasing order.

The lower quartile, denoted by
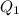`Q_(1)` is the median of the lower half of a data set

therefore, the lower half of the data is, {5, 7, 8, 11}, then the lower quartile is the median of {5, 7, 8, 11}

Since, the number of values is even, we need the median of the middle values to find the lower quartile i.e,
`Q_(1)=(7+8)/(2) =(15)/(2)=7.5`

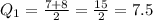
3)

First arrange the data in increasing order, {5, 7, 8, 10, 11 ,13, 14, 18, 27}

The upper quartile, denoted by
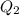`Q_(2)` is the median of the upper half of a data set.

therefore, the upper half of the data is, {5, 7, 8, 11}, then the upper quartile is the median of {13, 14, 18, 27}

Since , the number of values is even, we need the mean of the middle values to find the upper quartile, i.e
`Q_(3)=(14+18)/(2)= (32)/(2)=16`.

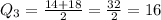4)

The interquartile range of of the data {5, 5, 6, 7, 9, 11, 14, 17, 21, 23}

The lower half of the data set is {5, 5, 6, 7, 9}

the upper half of the data set is {11, 14, 17, 21, 23}

The Lower quartile
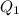`Q_(1)` of the lower half data is 6

the upper quartile
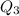`Q_(3)` of the upper half data is 17

The inter quartile of a data set is the distance between two quartiles i.e,
`Q_(3)-Q_(1)`
`=17-6=11`

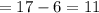
5)

The interquartile range of of the data {4, 5, 7, 9, 10, 14, 16, 24}

The lower half of the data set is {4, 5, 7, 9}

the upper half of the data set is {10, 14, 15, 24}

The Lower quartile
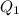`Q_(1)` is the median of the lower half data i.e,
`(7+5)/(2) =(12)/(2) =6`

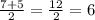
the upper quartile
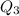`Q_(3)` is the mean of the upper half data is,
`(14+15)/(2) =(29)/(2) =14.5`

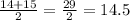
therefore, the interquartile of of the data {4, 5, 7, 9, 10, 14, 16, 24} is,
`Q_(3)-Q_(1)`=14.5-6=8.5