we are given
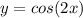
Since, we have to find inverse function
so, we will use following steps
step-1:
Set y=f(x)
It is already there
step-2:
Switch x and y
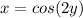
step-3:
Solve for y
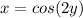
we can take cos^-1 both sides
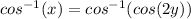
now, we can simplify it
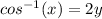
Divide both sides by 2
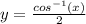
so, option-D........Answer