We will verify each options
option-A:
Inverse matrix:
we know that inverse matrix always exists for square matrix and non-singular matrix
non-singular matrix means

so, this is TRUE
option-B:
Inverse matrix:
we know that inverse matrix always exists for square matrix and non-singular matrix
non-singular matrix means

so, this is FALSE
option-C:
Inverse matrix:
we know that inverse matrix always exists for square matrix and non-singular matrix
non-singular matrix means

so, this is FALSE
option-D:
We know property of inverse matrix
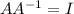
where I is the identity matrix
But this is not true for non-square matrix
so, this is FALSE