Answer:
b is the base of function which help us to determine the growth rate and Also tells the multiplicity of fishes .
Explanation:
Exponential Function:
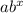 --1
--1
a = initial value (the amount before measuring growth or decay)
b>1 growth
b<1 decay
The growth "rate" (r) is determined as b = 1 + r.
The decay "rate" (r) is determined as b = 1 - r
After observing the population growth over a few weeks, the exponential function :
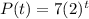
Comparing it with 1
b = 2
Since b >1
So, it is the growth function
So, The growth "rate" (r) is determined as b = 1 + r.
2 = 1+r
r = 1
Hence growth rate is 1
So, b is the base of function which help us to determine the growth rate and Also tells the multiplicity of fishes .