Question

Please, I need help!!

Answer 1

The box has weight 50.0 N (a downward force), from which we can determine its mass
`m`:

`-50.0\,\mathrm N=m(-g)=m\left(-9.80\,(\mathrm m)/(\mathrm s^2)\right)\implies m=5.10\,\mathrm{kg}`

The box's acceleration is taken to be uniform, which means its acceleration due to the frictional force (which acts in the leftward direction) at any time during the
`\Delta t=t_2-t_1=2.25\,\mathrm s` interval is

`\vec a=(0-1.75\,(\mathrm m)/(\mathrm s))/(2.25\,\mathrm s)=-0.778\,(\mathrm m)/(\mathrm s^2)`

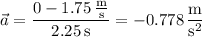
Then the friction force has magnitude
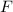`F` (where the vector is acting in the leftward direction) satisfies

`\vec F=m\vec a\implies-F=(5.10\,\mathrm{kg})\left(-0.778\,(\mathrm m)/(\mathrm s^2)\right)\implies F=3.97\,\mathrm N`

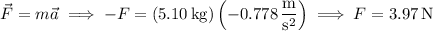
and the closest answer would be A.