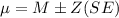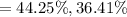Question

(1 point) A random sample of 600 movie goers in Flagstaff found 252 movie goers who had bought popcorn on their last visit. Find a 95% confidence interval for the true percent of movie goers in Flagstaff who have bought popcorn on their last visit. Express your results to the nearest hundredth of a percent. .

Answer:____ to____ %

Answer 1

A 95% confidence interval for the true percent of movie goers is 36.41% to 44.25%

Solution-

Given,

n = 600 (sample size)

x = 252 (number of people who bought)

Confidence interval = 95%, so z = 1.96

We know that,

`\mu = M\pm Z(SE)`

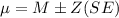
where,

M = sample mean

Z = Z statistic determined by confidence level

SE = standard error of mean

Calculating the values,

`M=(x)/(n) =(242)/(600) =0.4033`

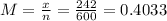
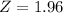`Z=1.96` from the tables

`SE=\sqrt{(M* (1-M))/(n)}`

`\Rightarrow SE=\sqrt{(0.4033* (1-0.4033))/(600)}=0.02`

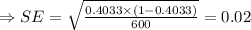
Putting all the values in the formula,

`\mu = M\pm Z(SE)`

`\mu = 0.4033\pm 1.96(0.02)`

`=0.4033\pm 0.0392`

`=0.4425, 0.3641`

`= 44.25\%,36.41\%`