Question

Which of the following graphs represents the equation y+2=3(x-1)

Answer 1

B

AND THE NUMBERS ARE (0,3)IS UP AND (1,1) ARE DOWN

WISH THAT HELP

سبحان الله ,الحمدالله ,الله اكبر

Answer 2

For this case we have the following equation, in a linear way:

`y + 2 = 3 (x-1)`

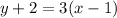
This expression can be written in the form
`y = mx + b`

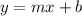
Where "m" is the slope and "b" is the cut point with the y axis.

Rewriting the given expression we have:

`y + 2 = 3x-3\\y = 3x-3-2\\y = 3x-5`

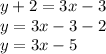
Thus, the slope is 3 and the cut point is -5.

To graph, we must find two points through which the line passes, so, we perform the following steps:

Step 1:

We do
`x = 0`

`y = 3 (0) -5\\y = 0-5\\y = -5`

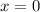
Thus, the point
`(x1, y1) = (0, -5)`

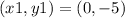
Step 2:

We do
`y = 0`

`0 = 3x-5\\5 = 3x`

`x =(5)/(3)`

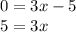
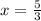
Thus, the point
`(x2, y2) = ((5)/(3),0)`

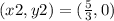
Answer:

See attached image