Answer:
Option B. 60300
Explanation:
The given expression
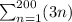 represents an arithmetic sequence. [3, 6, 9, 12,..............]
represents an arithmetic sequence. [3, 6, 9, 12,..............]
In this sequence first term a = 3
common difference d = 3
and number of terms n = 200
We have to find the sum of first 200 terms of this sequence.
Formula of the sum of an arithmetic sequence is
![=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2019/formulas/mathematics/high-school/m4c7t5iv8erxchwuheuuai90b7xm8fuf9k.png)
Now we put the values in the formula
![\sum_(n=1)^(200)(3n)=(200)/(2)[2(3)+(200-1)(3)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/7s3fgymsq7l7l7y7fm8qn0p1qe19nw7c74.png)
=
![100[6+(199)(3)]=100[6+597]](https://img.qammunity.org/2019/formulas/mathematics/high-school/a15hywp9a6eul6w4616se6umeubou12dj8.png)
=
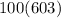
= 60300
Therefore option B. 60300 is the answer.