Answer: The correct option is 1, i.e.,
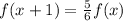 .
.
Step-by-step explanation:
The geometric sequence is in the form of,
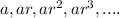
Where, a is the first term of the sequence and r is the common ratio of the sequence.
It means the
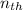 term of the sequence is defined as,
term of the sequence is defined as,
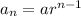
So the the
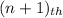 term of the sequence is defined as,
term of the sequence is defined as,
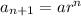

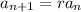
It means the geometric sequence is in the form of,

Where, r be any constant.
From the options only
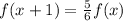 is in the form of
is in the form of
 with common ratio
with common ratio
 .
.
Therefore, the function can be used to model the graphed geometric sequence is
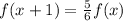 .
.