Question

I need help with this problem. Please answer and explain! (Ignore selected answer)

Answer 1

g'(0) = 1

Explanation:

The derivative of a function g at a number a, denoted by g'(a), is given by the definition of the derivative:

`\displaystyle g'(a) = \lim_(h\to0) (g(a+h) - g(a))/(h)`

In the definition of the derivative, "h" can be understood to be the horizontal change in the function with respect to a number a.

So g'(0) is

`\displaystyle g'(0) = \lim_(h\to0) (g(0+h) - g(0))/(h)=\lim_(h\to0) (g(h) - g(0))/(h)`

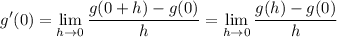
The variable in the limit is bound; without any other variables around, we can change the variable name to another reasonable variable name and it will still be the same. Hence we can change h to x and it will be equivalent:

`\displaystyle g'(0) = \lim_(x\to0) (g(x) - g(0))/(x) = 1`

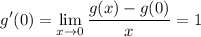
thus the given limit implies g'(0) = 1.