Question

What are the mean, variance, and standard deviation of these values? round to the nearest tenth.

Answer 1

A) mean = 47.6

variance = 31

standard deviation = 5.6

Explanation:

Answer 2

So this table is all about showing you how to calculate the standard deviation in various steps.

Step 1: calculate the average (=mean) of the x values. You probably know how to do this, add all values and divide by the number of values. (53+51+48+49+37)/5 = 47.6. This is your
`\overline{x}`.

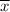Step 2: calculate
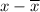`x - \overline{x}`. This is the "distance" of your x value to the average. This has been done for you already in the second column. E.g. 53-47.6=5.4.

Step 3: square the results of
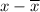`x - \overline{x}`. This is also done for you already, it is the third column.

Step 4: Add (sum) the
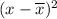`(x - \overline{x})^2` values. So add the third column. I get 155.2 when I do that.

Step 5: Divide that sum by the number of x values. 155.2/5 = 31.04 ≈ 31. That number is your variance right there!

Step 6: Take the square root of the variance. √31.04 ≈ 5.571 ≈ 5.6. This is your standard deviation.