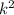Question

Rectangle ABCD is similar to Rectangle WXYZ . The area of ABCD is 30 square inches. Explain how to find the area, x , of WXYZ

Answer 1

Area of rectangle WXYZ = ( Area of rectangle ABCD ) /
`k^2`

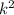
Explanation:

We know that two polygons are said to be similar if their sides are proportional.

As ABCD and WXYZ are similar,

`(AB)/(WX)=(BC)/(XY)=(CD)/(YZ)=(AD)/(WZ)`

Let this ratio be equal to k,

So,

`(AB)/(WX)=(BC)/(XY)=(CD)/(YZ)=(AD)/(WZ)=k\\AB=k\,WX\,,\,BC=k\,XY\,,\,CD=k\,YZ\,,\,AD=k\,WZ`

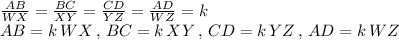
Area of rectangle ABCD = 30 square inches = length × breadth = AB × BC = k WX × k XY =
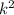`k^2` WX × XY =
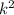`k^2` × Area of rectangle WXYZ.

So, if know value of k, we can find area of rectangle WXYZ

i.e, Area of rectangle WXYZ = ( Area of rectangle ABCD ) /
`k^2`